Quick sort is a comparison sort developed by Tony Hoare. Also, like merge sort, it is a divide and conquer algorithm, and just like merge sort, it uses recursion to sort the lists. It uses a pivot chosen by the programmer, and passes through the sorting list and on a certain condition, it sorts the data set.
How it works:
A pivot is chosen from the elements of the data set. The list must be reordered in such a way that the elements with the value less than the pivot come before it and the ones that are greater come after it. This is called the partition operation, and after this was completed, the pivot is in its final position, then, recursively, sort the rest of the elements.
Step by step example :
Having the following list, let’s try to use quick sort to arrange the numbers from lowest to greatest:
Unsorted list:
| 6 | 1 | 4 | 9 | 0 | 3 | 5 | 2 | 7 | 8 |
We go from START to END, with the pivot being the first element 6, and let us hide it. :
| 8 | 1 | 4 | 9 | 0 | 3 | 5 | 2 | 7 | 6 |
| i | j |
Now we scan with i and j. We have to find with i the first value greater than the pivot and with j the first value lower than the pivot. We found that the first value greater than the pivot is 8, and we are still looking for the first value lower than the pivot :
| 8 | 1 | 4 | 9 | 0 | 3 | 5 | 2 | 7 | 6 |
| i | j |
| 8 | 1 | 4 | 9 | 0 | 3 | 5 | 2 | 7 | 6 |
| i | j |
We found with j the number 2 which is lower than the pivot, so now we swap the elements pointed by i with j:
| 2 | 1 | 4 | 9 | 0 | 3 | 5 | 8 | 7 | 6 |
| i | j |
Now, we look again for greater values than the pivot with i:
| 2 | 1 | 4 | 9 | 0 | 3 | 5 | 8 | 7 | 6 |
| i | j |
We found the element of 9 which is greater. Now we seek an element lower with j:
| 2 | 1 | 4 | 9 | 0 | 3 | 5 | 8 | 7 | 6 |
| i | j |
We found 5. Now we swap them:
| 2 | 1 | 4 | 5 | 0 | 3 | 9 | 8 | 7 | 6 |
| i | j |
We begin the search again, but this time, the index i passes over the index j, so this means at the position where i is the index is the proper place for the pivot, and we swap the value of the pivot with the value that is currently there:
| 2 | 1 | 4 | 5 | 0 | 3 | 9 | 8 | 7 | 6 |
| j | i |
| 2 | 1 | 4 | 5 | 0 | 3 | 6 | 8 | 7 | 9 |
| j | i |
If you look closely, all the elements before 6 are smaller and all the elements after the former pivot are greater. Now, we split the initial list into two smaller lists according to the former pivot: 2, 1, 4, 5, 0, 3 and 8, 7, 9. We repeat the same procedure for each of the sub-lists. The pivot will be the first element in each case, and when the proper place for the pivot was discovered and moved in accordance to this, again we split the list into two smaller ones using the same rule: one list will be composed by the elements smaller than the pivot and the next list composed by elements greater than the pivot. By the end, the initial list will be put together and it will be sorted.
Sample code:
#include < iostream >using namespace std;
void swap(int &a,int &b)
{int aux;
aux = a;
a = b;
b = aux;
}int partition (int *a, int low,int high)
{int l = low;
int h = high;
int x = a[l];
while (l < h)
{while ((a[l] <= x) && (l <= high))
l++;
while ((a[h] > x) && (h >= low))
h--;
if (l < h)
swap(a[l], a[h]);
}swap(a[low], a[h]);
return h;
}void QuickSort (int *a, int low, int high)
{int k;
if (high > low)
{k = partition(a, low, high);
QuickSort(a, low, k-1);
QuickSort(a, k+1, high);
}}int main()
{int n;
int *a;
cout << "Please insert the number of elements to be sorted: ";
cin >> n; // The total number of elements
a = (int *)calloc(n, sizeof(int));
for(int i=0;i< n;i++)
{cout << "Input " << i << " element: ";
cin >>a[i]; // Adding the elements to the array
}cout << "Unsorted list:" << endl; // Displaying the unsorted array
for(int i=0;i< n;i++)
{cout << a[i] << " ";
}QuickSort(a, 0, n-1);
cout << "nSorted list:" << endl; // Display the sorted array
for(int i=0;i < n;i++)
{cout << a[i] << " ";
}return 0;
}
Output:
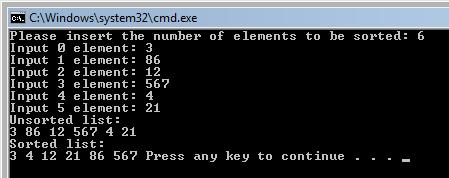
Code explanation:
The partition function does what it is called, it chooses the pivot, then, like in the example, while l is smaller than high (or i smaller than j like in the example) it checks the list for the elements that must be greater or smaller, and when it has found them, a swap function is executed. Then, inside the QuickSort function, after the pivot was found, the list is divided into two smaller lists, according to the pivot, then recursively the partition function is called for each sub-list and in the end the initial list is sorted.
Complexity:
Time
In the best case, the partitions are of equal size at each recursive call, and there are then log2(n) levels of recursive calls. The whole array is scanned at each level of calls, so the total work done is O(N*log(N)).
The average time complexity is also O(N*log(n)).
The worst case time complexity is O(n^2). This occurs when the estimate of the median is systematically always poor, e.g. on already sorted data, but this is very unlikely to happen by chance.
Space
As coded above the best- and average-case space-complexity is O(log(N)), for the stack-space used.
The worst-case space-complexity is O(N), but it can be limited to O(log(N)) if the code is modified so that the smaller half of the array is sorted first (and an explicit stack, or the tail-recursion optimization used).
In that case, the best-case space-complexity becomes O(1) .
Advantages:
- One of the fastest algorithms on average;
- Does not need additional memory (the sorting takes place in the array – this is called in-place processing).
Disadvantages:
- it The worst-case complexity is O(N2);
- is recursive;
Conclusion:
Commercial applications use Quicksort – generally it runs fast, no additional memory, this compensates for the rare occasions when it runs with O(N2). Never use in applications which require guaranteed response time:
- Life-critical (medical monitoring, life support in aircraft and space craft)
- Mission-critical (monitoring and control in industrial and research plants handling dangerous materials, control for aircraft, defense, etc)
unless you assume the worst-case response time.
[catlist id=197].
